





( Concerne les variations de volume et pression lors d'une transformation d'une quantité fixe de gaz à température constante).
Le piston permet de faire varier le volume, le manomètre mesure la pression:

Résultats:
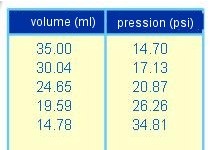
En multipliant la pression par le volume, on trouve toujours le même résultat!
$P \cdot V = k_1$ où $k_1$ est un nombre constant à une température donnée.
En d'autres mots, pour le même gaz à température donnée, en passant d'un état 1 (pression $P_1$, volume $V_1$) à un état 2 (pression $P_2$, volume $V_2$), on a:
À température constante: $P_1 \cdot V_1$ $=$ $P_2 \cdot V_2$ ( = $k_1$)
( Concerne les variations de volume et température lors d'une transformation d'une quantité fixe de gaz à pression constante).
Le réchaud permet de faire varier le volume, un thermomètre interne mesure la température:

Résultats:

La fonction V=f(t) est une droite coupant l'axe des températures au point d'abscisse $-273,15^oC $
Si nous définissons une nouvelle échelle des températures par:
Température absolue = Température Kelvin = $T$ $=$ $273,15$ $+$ $t(^oC)$
alors l'origine de cette échelle $T = 0 K$ se situe à $-273,15^oC $ et le graphique V=g(T) sera celui d'une droite passant par l'origine:
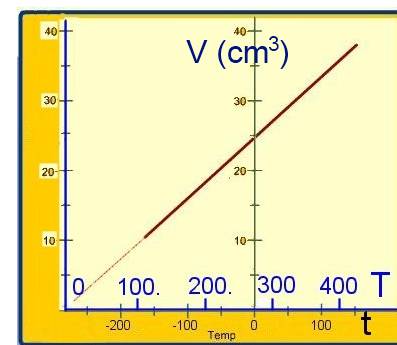
$V = k_2T$ où $k_2$ est un nombre constant à une pression donnée
En d'autres mots, pour le même gaz à pression donnée, en passant d'un état 1 (température absolue $T_1$, volume $V_1$) à un état 2 (température absolue $T_2$, volume $V_2$), on a:
À pression constante: $\frac{V_1}{T_1}$ $=$ $\frac{V_2}{T_2}$ ( = $k_2$)
( Concerne les variations de volume, pression et température lors d'une transformation d'une quantité fixe de gaz) .
Envisageons une transformation quelconque d'un gaz d'un état 1 vers un état 2:
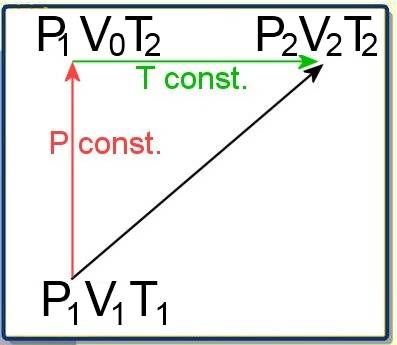
Soient $P_1$ , $V_1$ et $T_1$ la pression , le volume et la température à l'état 1. Soient $P_2$ , $V_2$ et $T_2$ la pression , le volume et la température à l'état 2. Le passage de 1 à 2 peut se faire aussi par un détour consistant en une transformation à pression constante (a) suivie d'une transformation à température constante (b) (a)$\frac{V_1}{T_1}$ $=$ $\frac{V_0}{T_2}$ (Gay-Lussac) (b)$P_1\cdot V_0$ $=$ $P_2\cdot V_2$ (Boyle-Mariotte) En éliminant $V_0$ entre (a) et (b), on trouve:
$\frac{P_1\cdot V_1}{T_1}=\frac{P_2\cdot V_2}{T_2}$
( Concerne la description de l'état d'un gaz: volume, pression, température et nombre de moles)
.Considérons une mole de gaz. La loi précédente est valable: $\frac{P_1\cdot V_1}{T_1}$ $=$ $\frac{P_2\cdot V_2}{T_2}$ Donc pour n'importe quelle température et pression et pour une mole de gaz, le produit $\frac{P\cdot V}{T}$ reste constant: $\frac{P\cdot V}{T}$ $=$ $R$ $V$ $=$ $R\frac{T}{P}$ où $R$ est une constante pour une mole de gaz qui ne dépend plus de la température, ni de la pression) $R$ $=$ $0,082\frac{l\cdot atm}{mol\cdot K}$ si $P$ est exprimé en atmosphères et $V$ en litres $R$ $=$ $8,3\frac{N\cdot m}{mol\cdot K}$ si $P$ est exprimé en Pascal ($\frac{N}{m^2}$) et $V$ en $m^3$ Pour n moles de gaz par contre, sous les mêmes conditions de pression et de température, d'après la loi d'Avogadro, le volume sera n fois plus grand: $V$=$n\cdot R\frac{T}{P}$ ou encore:
$P\cdot V$ $=$ $n\cdot R\cdot T$ avec $R$ $=$ $0,082\frac{l\cdot atm}{mol\cdot K}$ si $P$ est exprimé en atmosphères et V en litres $R$ $=$ $8,3\frac{N\cdot m}{mol\cdot K}$ si $P$ est exprimé en Pascal $(\frac{N}{m^2})$ et $V$ en $m^3$
( Concerne le volume et nombre de moles d'un gaz à 0oC et 1 atm = les conditions normales de température et de pression)
.Appliquons la loi des gaz parfaits (forme 2): $P\cdot V$ $=$ $n\cdot R\cdot T$ $1\cdot V$ $=$ $n\cdot 0,082\cdot 273,15$
À 0oC et 1 atm (c.n.t.p.): $V$ $=$ $n\cdot 22,4$ où $V$ est exprimé en litres